【转帖】怪老子: 如何評估股票價值
Tan KW
Publish date: Thu, 28 Mar 2013, 10:06 AM
當我們買一張股票時,最常碰到的問題是這張股票到底值多少錢?或者用另一角度來問,為何台塑股票80元你願意買?的確!很少人心中有個底,知道想購買的股票實際值多少錢。大部分人買股票的原因是:“覺得”這檔股票會漲,然而這不禁讓我們心中有個疑問,難道沒有一種比較有學理的方法,能夠計算股票的內在價值嗎。
有一種評價模式是假設買了股票後永遠持有,那麼這股票終身所配回股息折成現值後的總額,就是這股票的價值。這種評價模式的確相當合理,雖然股價會隨著股票市場喊價而波動,但追根究底投資者不就是為了配息而買股票嗎,所以從配發股息著手的確是釜底抽薪的辦法。當知道這股票的內在價值後,心中就會有個定見,到時進可攻退可守,就算股票套牢,靠著配發股息也是個不錯的投資。
理論模型
接下來會有些數學部份,但請放輕鬆的看過,這兒只會交代公式的意義,不會有艱澀的運算。運算部分交給Excel來做就好了,不必我們煩心。
若未來每年的現金股息分配,第1年配股息D1,第2年配股息D2,依此類推第n年配股息Dn,那麼將這些未來可能分配的股息以投資者期望報酬率R折成現值,加總後就是該股票之價值:
P0 = D1/(1+R)1 + D2/(1+R)2 +D3/(1+R)3 +‧‧‧ -----------------------(公式一)
這就是投資學上的股價評價通用公式。式子裡第1項D1/(1+R)1是第1年股息D1之現值,第2項D2/(1+R)2是第2年股息D2之現值,依此類推。所以我們只需依序將每個配息之現值一個一個分別算出來就好了。可是~~~~有無窮多項耶,那不算死人了嗎?放心!有Excel代勞,不用1秒鐘答案立即出現。
實務演練
理論看起來很簡單,可是怎知道未來每年分配的股息是多少,尤其是獲利成長公司,每年的盈餘不斷的推升,這樣又是如何算呢?就是因為無法準確預測長時間的股息分配,所以學術界就發明了一些理論模型(附註一)來分析股票價值,一個是零成長模型,假設每年配息金額都一樣;另一個是成長模型,假設每年配息以一定比例成長。兩者也都是根據公式一所演繹出來的。這些理論其實和股票實務脫節蠻深的,有哪一檔股票是永遠配發同等配息的,或有哪一檔股票的配息會永遠以一個固定成長率往上飆高。正常公司的成長曲線不會是直線型,在需求強勁時會以較高的成長率往上爬,到一定時候時成長會較為遲滯,在過一些年後會市場飽和就不再成長了。有了Excel的強大試算功能,利用公式一的觀念,就可輕易計算出股票價格,而且成長率可以每年任意調整反覆試算。
Excel試算表下載
這兒提供一個Excel檔案供下載,裡面有本文談到的範例,讀者也可自行利用本文談到的方法,將資料直接套入即可。
觀察最近10年成長率
Excel雖然提供了極佳的計算能力,但是我們還是得預測未來的成長率到底是多少,因為成長率決定股票價值頗巨,所以必須謹慎估算。最好的方式是先了解過去成長情形,再加上最近的研究報告,便比較容易預測未來股息成長情形。最近幾年的股息配發資料網路上應該都不難取得,根據這些資料再做一些運算,就可以得到有用資訊。計算方式是先將每年的配息金額加計配發股票股利後的“實領配息”,再算出每年平均成長率當作未來成長率之參考。有了這些資料,對未來的配息預測是很有幫助的。
考慮股票股利之影響
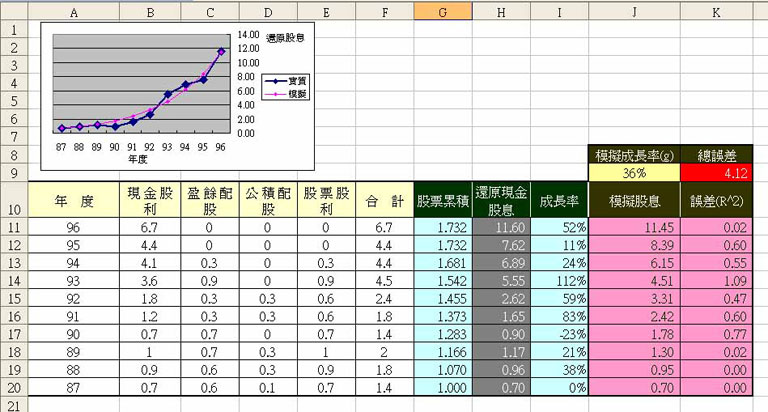
圖(一)是台塑公司最近10年的股利配發情形(儲存格A10~F20),這些資料讀者可以從Yahoo股市裡下載,可是這些股利及股息配發資料,並不能拿來直接用,因為第1年所買的1股,到了第2年因為配發股利的關係已經不只有1股。如果去年配發股票股利為1元,那代表今年的股票數量會增加10%,就是去年1股今年增加0.1股,總共擁有1.1股。所以必須加計因股票股利所累積的股數,再乘上當年的配息金額,才是當年的配息收入。『還原現金股息』那一欄,就是將股票股利因素考慮在內的實領配息。
下表是圖一欄位的詳細說明。
| 欄位標題 | 儲存格 | 說明 |
| 股票累積 | G欄 | 假設87年買的1股,到了該年度所擁有的股數 |
| 還原現金股息 | H欄 | 實質領取股息 = 該年股票累積 * 現金股利 |
| 成長率 | I 欄 |
根據還原現金股息,和去年相比之成長率 = (今年股息-去年股息)/去年股息 |
| 模擬成長率 | J9 | 模擬股息所根據的成長率之計算參數,意義相當於平均年成長率 |
| 模擬股息 | J11~J20 |
計算去年股息以模擬成長率得到之金額 = 去年股息*(1+模擬成長率) |
| 誤差 | K11~K20 |
將模擬股息之當年金額和還原現金股息相減,就是求取這兩者之差距,再平方以得到差距之正值。 = (模擬股息-還原現金股息)2 |
| 總誤差 | K9 | K11~K20之總和,目的是希望得到一個誤差最小的模擬成長率 |
求出配息平均成長率
儲存格J9是模擬成長率,目的是想得知台塑近10年的配息平均年成長率是多少?如何可以得到這個值呢?先給一個模擬成長率g(J9),再做一個模擬股息欄位(J欄)。87年模擬配息的起始值(J20)應該和87年的還原現金股息(H20)一樣,87年之後的模擬配息,每年都是“固定”乘上去年配息的(1+g)倍。
整個涵意是說若有一『成長模型』,以87年的配息為起始點,每年平均都以g成長率爬升,那麼只要比較台塑近10年的實際配息,和『成長模型』的成長率g,看那一個最為接近。
例如台塑87年之股息(J20)為0.7元,模擬配息是每一年都“固定”以模擬成長率(J9)成長,亦就是每年之配息都是去年的(1+g)倍。若g為36%:
87年 = 0.7
88年 = 0.7*(1+36%) = 0.96
89年 = 0.7*(1+36%)*(1+36%) = 1.30
90年 = 0.7*(1+36%)*(1+36%)*(1+36%) = 1.78
.....
台塑近10年的實際配息和g=36%這組最為接近了,所以也可以說過去10年配息,平均每年以36%成長。但要注意的是~~~歷史資料不代表未來也會如此。
如何比較實際配息和成長模型,就是利用誤差欄(K欄),來檢驗由模擬成長率g算出的『模擬股息』,和實際『還原現金股息』的誤差有多大,然後反覆調整模擬成長率g達到兩者最低的誤差值。誤差計算方式是將當年“模擬股息”減去“還原現金股息”,再求其平方以取得正值。總誤差(K9)就是所有誤差(K11~K20)之總和。
這樣我們就可以用代入法來求得最接近實際配息的一個成長率,做法如下:
1) 先隨便猜一個模擬成長率(J9),例如20%好了,這時總誤差(儲存格K9)算出來的結果是117,而且模擬股息(圖一粉紅色曲線)看起來和實質股息會有些差異。
2) 試著上下改變儲存格J9的數值,看那一個數字會得到最小的總誤差(K9),那個成長率就是最接近10年的平均成長率。
▼圖(一)台塑公司最近10年的股利
利用Excel規劃求解工具
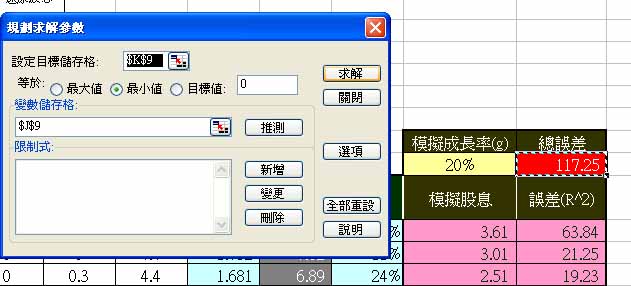
其實不用那麼累,一個一個值去試試看,可以利用Excel的規劃求解,就可以輕鬆得到平均成長率。方法如下:
1) 下拉選單=>工具=>規劃求解,會出現如下圖視窗。若工具裡找不到『規劃求解』選項,必須到工具=>增益集裡將『規劃求解』選項打勾才行。
2) 『設定目標儲存格』==>$K$9,『等於』==>“最小值”,『變數儲存格』==>$J$9
3) 按求解後,如出現“規劃求解找到一解‧‧‧”,選『保存運算結果』,再按『確定』即可
▼圖(二)規劃求解參數設定
計算股票價值
當最近10年的平均年成長率知道後,就可以開始預估未來的配息成長囉,利用公式一的通用公式
P0 = D1/(1+R)1 + D2/(1+R)2 +D3/(1+R)3 +‧‧‧
公式一的每一個加項,就是每一年的股息經折現後之現值,第1年股息為D1,除以1年折現因子(1+R)1,就是第一年股息之現值。第2年股息為D2,除以一年折現因子(1+R)2,就是第2年股息之現值,依此類推。
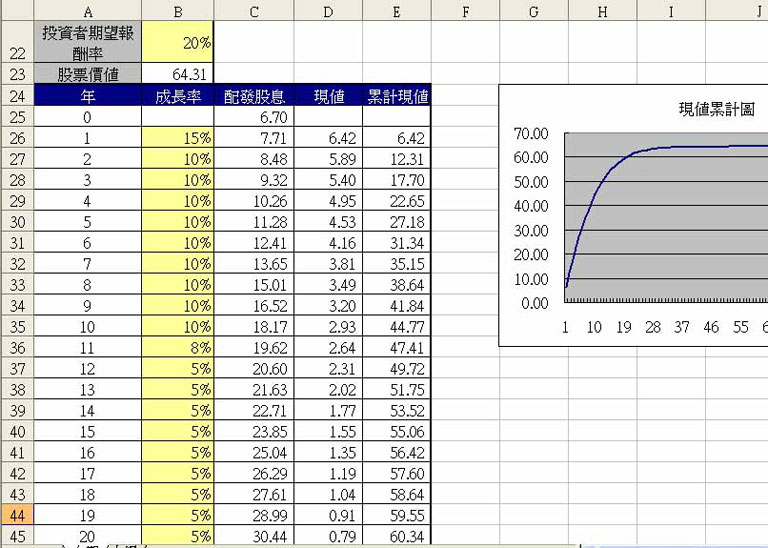
可是~~~~這式子不是無窮級數嗎?Excel如何計算無窮級數。不用擔心,雖然是無窮級數,但是每一年的股息都要除以(1+R)n來折成現值,愈久的年數n的值愈大,除數成指數增加,現值就會變得很小。也可以這麼解釋,就是很久以後所拿到的股息對現在股價是沒啥影響的。圖三有一個『現值累計圖』,就是將每年股息現值累計相加的圖,可以看出到25年後,已經不再增加了,因為25年後股息的『現值』那一欄(D欄)的數值幾乎都等於零。這也說明了25年後股息之多寡,對現在的股票價值是無關緊要的。
雖然如此為了增加準確度,Excel還是計算了100年的股息。根據每年的成長率預測來計算,然後一一根據期望報酬率以年數(1+R)n折成現值,再將所有現值加總,就是股票價值了(B23)。
成長率欄(B26以後的黃色儲存格)必須讀者自行填入,這也是最具挑戰性的地方,讀者已經知道過去10年的平均年報酬率了,這時候就得預測未來100年的成長率了(B26~B125)。什麼!預測100年。別大驚小怪,我知道是不好預測,但是總得猜一個,要不然如何算,事實上外資那些專業分析師也就是預測這些值。
妳只要專心的猜未來25年內的成長率,尤其是10年內的成長率,因為影響最大。25年後大概市場也飽和,填0%或5%都無坊了。模擬成長率(J9)已經算出過去10年的平均成長率,讀者可根據這數值,加上對該公司的客觀了解,去猜這數值。
配發股息欄(C26~C125)會根據讀者推定之成長率,算出當年配發股息。現值欄(D26~D125)將當年之股息以投資者期望報酬率(B22)一一折成現值。D26~D125的每一儲存格,代表著式子(一)的每一項。股票價值(B23)是將每年配發股息(D26~D125)加總,相當於式子(一)的P0,也就是我們要的結果。
▼圖(三)台塑股票價值及成長率預測
分析及討論
評價模式做出來了,接著就用現有股票來做一下分析,拿台塑股票來說吧,今天(2008/8/18)股價64元,如果設定投資者預期報酬R為20%(股票要求這等報酬率應該不為過),那麼則必須將未來成長預測壓低至10%~15%左右(如圖三所示),股價才會等於64元。可是上述分析告訴我們,台塑近年來的配息成長率高達36%,而且還正在成長中,所以我認為台塑股票目前是明顯低估。
成長緩慢的公司
再舉中鋼公司為例(下載Excel裡有資料),用同樣方法來看近10年配息,可以得知過去成長率每年平均6%。若中鋼未來20年配息還是以6%成長,算出來結果也只值27元,相較今天的股價37.9元,我認為是明顯高估。台塑跟中鋼這兩張股票,我肯定選擇台塑。
成長率決定股價
由這方法可以看出,股價是由最近30年的股息配發來評價的,而且股息成長率影響股價頗大,這也是為何當一檔股票之成長率超乎預期時,股價就一直往上漲的原因。
本益比迷思
買股票有一個量化指標叫做本益比,就是股價除上每股盈餘。盈餘是當年的,所以本益比沒有任何未來成長與否的資訊,就是說今年的盈餘不代表未來也會一樣。所以不是本益比小,就代表這股票便宜。通常低本益比的公司,就是因為成長率低,所以被專業機構評定低股價,所造成的低本益比。所以不是低本益比的股票就是好股票。
附註一:投資學上的分析方法
配息零成長評價公式
一家公司市場成熟穩定不會再有成長,所以每年配息都非常穩定,配發一定的股息D,若期望的投資報酬率是R,那麼未來領取股息的現值如下:
P0 = D/(1+R)1 + D/(1+R)2+ D/(1+R)3+‧‧‧
=D*(1/(1+R)1 + 1/(1+R)2+ 1/(1+R)3+‧‧‧)
=D/R ---------------(公式二)
例如A公司每年都配發股息3元,投資者的期望報酬為R,所以這股票價值= 3 / R ,那麼股票價值和投資者的期望報酬有關,不同期望報酬率的股票價值如下:
|
報酬率(R)
|
投資者願意購買價
|
|
10%
|
30
|
|
15%
|
20
|
|
20%
|
15
|
|
30%
|
10
|
也就是說同樣的每年都拿到3元的股息,因為投資者的預期報酬率不同,所願意付出的價格也會跟著不一樣。
用Excel來計算
這種配息零成長的特例,不需要用公式計算,直接把值代入本文所附的Excel,答案立即出來且跟投資學的公式一模一樣。股息(C25)輸入3,把B26~B125都輸入0%,就是說100年都不成長每年都是3元配息,投資者的期望報酬(B22)輸入20%,那麼股票價值(B23)應該跟下列公式一樣是15元。
P0 = D/R = 3/20% = 15
有興趣讀者可以自行驗證一下。
獲利成長評價公式
若一家公司的獲利是正在成長,亦就是一年比一年還要多,當然配息也是一年比一年多,這樣類型的公司,股價該如何來評定呢?若股利每年以g成長,也就是每年股利配發都是去年的(1+g)倍,投資者的期望報酬為R,通用式子可以得到:
P0 = D1/(1+R)1 + D2/(1+R)2 +D3/(1+R)3 +‧‧‧
= D0(1+g)1/(1+R)1 + D0(1+g)2/(1+R)2 + D0(1+g)3/(1+R)3+‧‧‧
P0 = D0*(1+g)/(R-g) = D1/(R-g) ---------------(公式三)
=>條件是:g必須小於R
這也稱為股利成長模型(Dividend Growth Model)。
舉例說台塑今年配發股利6.7元,若每年以8%成長,投資者的期望報酬為20%,
那麼台塑的股價應該是:=6.7*(1+8%)/(20%-8%) = 60.3元。
用Excel來計算
本文所附的Excel是通用的,每年成長率都可變更,當然也適用這模型的計算。股息(C25)輸入6.7,把B26~B125都輸入8%,就是說100年每年都以8%成長,投資者的期望報酬(B22)輸入20%,那麼股票價值(B23)答案是60.3元,應該跟上面公式所算出的結果是一模一樣。除了可看到答案外,還可以看到每年的配息狀況,以及配息之折現。細心讀者會發現到最後雖然配息金額非常龐大,可是折現後卻等於零。這也可以從現值累積圖看出,30年後的配息雖多,但已經沒有貢獻度了。
My trial on AEON @ Google Doc
http://www.masterhsiao.com.tw/StockValuation/StockValuation.htm
More articles on Good Articles to Share
Created by Tan KW | Jan 08, 2025
Created by Tan KW | Jan 08, 2025
Created by Tan KW | Jan 08, 2025



















Jordan Ching
thank you again
2013-03-30 21:35