[转贴] 有錢人的決策思維：搞懂「概率權」是成功的開始？

什麼是概率權？概率權是我創造的一個詞。概率權，是基於機率計算的未來選擇權。

塔勒布和交易員勞倫共進晚餐，兩人擲硬幣決定由誰付帳，塔勒布輸了，只好乖乖掏出腰包。勞倫本來想道聲謝，卻突然改口說： “ 看了你的書，我想你一定會說，在機率上，這頓飯我付了一半的錢。 ” 理解這一點並不容易，有些人寧可追求比被雷劈機率還小的中獎機會，也不願意去做有 50% 把握成功的事情。

概率權與未來有關。2020 年 3 月份爆賺 30 倍的基金經理斯皮茨納格爾在《資本的秩序》裡寫道：

資本具有跨期特徵：它的定位和在未來不同時點的優勢是核心。

時間是資本的生存環境——定義它、塑造它、幫助它、阻礙它。

我先將概率權搭個簡單的框架，以督促自己早點兒寫一篇完整的。

基於期望值計算的（與空間有關的）概率權。
歷史上贏得了彩票的人，都是利用了彩池偶然出現的正期望值。所以他們抓住機會拼命買，買的越多，越接近於大數定律下的期望值。另外一方面絕對收益也更大。但是，如果面對負的期望值，再死磕，也沒用。勤奮對於賭博和買彩票這類期望值為負的事情毫無意義。
基於貝氏更新的（與時間有關的）概率權。
創業上的快速試錯，是希望透過貝氏更新，不斷優化商業模式上的機率，直至發現正期望值的套利機會。厲害的人，會不停扔骰子，去看骰子怎麼說。這就是蒙特卡洛的仿真模擬，在一個可以收斂的半徑內，聰明地犯錯誤。不僅從別人那裡學習，還敢於親自當骰子。貝氏學派相信模擬不確定性是學習的關鍵，並利用貝氏網路和馬爾科夫網路來工作。
基於三層結構的概率權。
這三層分別是資源層、配置層、執行層。世俗世界的最終結果取決於三者機率相乘的結果。
在一個博弈環境中製造有相對優勢的（基於統計學的）概率權。
放棄追求所謂最優，只在乎發現相對的機率優勢。這是一種套利思維。有時候，利用的是對機率計算的認知優勢；有時候，利用的是競爭對手對不確定性的恐懼感。
概率權還是 “ 無所不知者 ” 對機率的分配權。
例如，流量、IP 等等，背後其實都是平台的概率權分配遊戲。所以，最好的商業模式，尤其是那些平台型商業，本質上是製造了一個 “ 賭場 ” 。如此一來，平台就成為概率權的設計者，和分配者。

懂機率的人，人生都不會太差

據推測，翻車魚從一枚受精卵發育成成魚的機率只有百萬分之一。
那該怎麼辦呢？秘密武器是：機率。一條中等體型的翻車魚一次性就能產下 3 億個卵，是脊椎動物中產卵數量最多的。這種長相奇怪的魚，用這種方式頑強地繁衍了下來。從生命到宇宙萬物，假如真有造物主，他主宰的工具就是機率。
機率，在我看來是對一個人最有價值的數學知識，然而我們並沒有認真學過這門課程。
為什麼呢？因為：
a、懂得機率計算，未必具有機率思維；
b、理解機率思維，又未必能夠採取機率行動。
人們不願意計算。尤其是不願意計算機率。更多時候，人們喜歡採用啟發式思考，用深藏在記憶中的、被我們編織起來的故事，來取代更精確的機率判斷。
現實中，絕大多數人，黑白分明、非此即彼，但現實是灰度的。
機率就是用來精確描述和運用這種灰度的。蔡崇信說過： “ 任何機會，基本上是有 30% 把握去做的時候才能贏得最大——因為機率太小很可能虧本，而有 50% 把握的時候，贏了基本也是小贏；而有 80 %把握去做的時候，基本就是紅海了；如果等到 100% 機會的時候⋯⋯。世界上可能根本沒有這種生意。 ” 當然，這背後還需要入場後的貝氏更新。
即使是極度厭惡不確定性的巴菲特，其價值投資也會出錯，只是長期而言賺錢的機率更高。認識了機率，在行動上就不過度追求完美。我們往往必須在資訊不完整的前提下做出決策。
投資和人生，都是對不確定性的處理。我們要為犯錯做好準備。也要適當的冒險，這是一種或然性思維。
人們總是容易高估自己與眾不同，也會經常幻想 “ 這一次真的不一樣 ” 。然而很多事情真的很難跳脫機率。例如，你要出版一本書，先別想自己能不能做成這件事，以及計劃多長時間做完，先去問一下做出版的朋友，這件事以前的成功率是多少？（卡尼曼講過類似的故事。）
這個世界從物質的角度看，也受機率支配。
量子世界的本質是機率的。牛頓力學的嚴格因果關係在量子世界並不存在。費曼說，這有點兒讓人沮喪，但物理學並沒有因此垮台。
機率從何而來？
想要回答這個問題，我們要追溯至數學、物理和哲學。這三者，探索的都是世界的本源問題。很遺憾，我們的教育，沒有通識這一塊。所以，想要真正理解機率，對於成年人而言極其艱難。
我們需要按照機率行事。
要想改變世界，首先要改變自身的機率結構。人生的絕大多數時候，量變不會產生質變，你會被大數定律牢牢地鎖死在機率劣勢（或優勢）中。就像愛因斯坦對愚蠢的定義：重複做一件傻事，卻指望得到不同的結果。行事方式（你的機率結構），比聰明與否和經驗都更重要。
段永平談及 “ 怎麼保證選對人 ” 這個問題時說：沒有絕對的辦法來保證，但如果選人時先看合適性（價值觀匹配）會比只看合格性（做事情的能力）要好得多，選中合適的人的機率要大得多。看，無處不在的機率。
斯賓諾莎說：幸福並不是美德帶來的報酬，而是美德本身。
我們遵循機率，未必一定會有好的結果。因為命運會用惡作劇捉弄機率。但這並不影響我們由此獲得的從容和幸福。此外，為了讓自己不被偶然戲弄，我們要努力從賭徒模式升級為賭場模式，讓大數定律為自己服務。
諾獎得主蓋爾曼說：宇宙的歷史並不只是由基本定律決定的。它取決於基本定律和除此之外的一長串巧合或者說機率。基本理論並不包含那些機率，它們是額外的東西。因此它並不是萬物理論。實際上，宇宙中圍繞我們的大量資訊來自於這些巧合，而不只是基本定律。現在人們常說，透過檢驗由低能量到高能量再到更高能量，或者說由小尺度到更小尺度再到更小尺度的現象來逐步向基本定律靠近就像是剝洋蔥。
我們這麼不斷繼續下去，建更高能的加速器來找尋基本粒子，這樣就能夠逐步深入粒子的結構，沿著這條路，我們就可以逐漸接近基本定律。
人生贏家都是機率贏家。
他們不是走了超級狗屎運，不然就是洞悉了巧合背後的基本定律。大部分人屈服於命運，少部分人與命運抗爭（作為他們命運的一部分），極少人試圖去發現命運的把戲。總之，機率思維，已經成為當今在社會上行走必備的基礎能力。

機率統治世界

時間只負責 “ 統計 ” ，不負責 “ 判決 ” 。機率層面，這是簡單的常識：

假如一個不規則的硬幣落在正面的機率是 55% ，你下注於正面。結果，硬幣落在了反面。你輸了錢。時間並沒有說：你錯了。時間的意義是，你不斷重複這個遊戲，最後你有 55% 的機率贏。

可是，我們對時間最大的誤解，就是以為它是最英明的裁判。例如，一個阿根廷的孩子在街頭踢球，他熱愛，聰明，但又脆弱，各種坎坷，甚至被認為沒有前途。可他後來成了梅西。通常我們會認為，時間 “ 證明 ” 了梅西的成長，它肯定了這個孩子的天賦和努力。然而，時間並不是這樣一個高考閱卷老師。時間只是從統計學意義上，觀察到梅西的湧現。

即使時間是萬能的，但是在梅西小時候，它對小梅西成為梅西這件事情，和每個人一樣一無所知。理解了這一點，我們就知道，假如我們想要培養梅西，無法靠 “ 我早就知道 ” 的設計，而是要靠基於 “ 演變 ” 的統計。統計，將 “ 偶然 ” 和 “ 命中註定 ” 聯繫在了一起。《自下而上》寫到：

人類歷史的傳授方式，也由此充滿了誤導，因為它太過強調設計、指導和規劃，而太少關注演變。所以，打了勝仗的，是將軍；經營國家的，是政客；發現真理的，是科學家；創造流派的，是藝術家；實現突破的，是發明家；塑造心靈的，是老師；改變思想的，是哲學家；佈道的，是教士；做生意的，是商人；陰謀導致危機⋯⋯。

於是，有人呼喚 “ 我們需要天才馬斯克 ” ，卻不知道，也許創造奇蹟的，是一代在後院兒玩兒土火箭的少年，是大量專業的太空發燒友。只有當街頭有很多光著腳快樂踢球的孩子時，才有機會 “ 湧現 ” 出梅西。過去，我們想把幾十個天才足球少年送去歐洲和南美，定向培養出馬拉多納。現在，人們又指望定向製造馬斯克。

我也並非徹底推到 “ 規劃 ” 。例如日本就曾經規劃 “ 諾貝爾獎得主 ” 。但這個 “ 規劃 ” ，是 “ 自下而上 ” 與 “ 自上而下 ” 的結合。是去 “ 規劃 ” 一整片森林，而非定向規劃少數幾棵看起來大有前途的天才樹木。模糊的精確，好過精確的模糊。在一個複雜的世界裡， “ 因 ” 這個概念本身就值得懷疑： “ 這就是別太在乎報紙說什麼的另一個原因，它們總是無休無止地為事情找原因 ” 。

時間容易造成 “ 前因後果 ” 的幻覺。因為時間的單向、線性、均勻，都只是人的一個幻覺。時間也許更像大爆炸的宇宙，向四面八方加速地展開。甚至於，時間本身的維度，也遠不止我們心智中的三維，並且連維度的數目也在 “ 分裂 ” 。所以，在一個開放的系統裡，試圖透過極其有限的數據與觀察來發現 “ 絕對的因果 ” ，極可能是錯的。當然，我上面一大段對時間因果的懷疑，仍然是在人類語言和思維模式的因果框架下展開的。

我贊成不要因為 “ 統計學 ” 在這個時代格外有效，就放棄對 “ 因果 ” 的探究（其本質是求真，並且避免陷入虛無）。牛頓力學不夠精確，但已經能確保我們的房屋與橋樑的相對牢固；量子力學充滿疑惑，卻構成了手機和網路的基石。假如我們接受時間負責 “ 統計 ” ，而不是 “ 裁判 ” ，就能夠做到：既追求真理，又保持懷疑；既享受一生（極小的一段時光）牢靠的幻覺，又能將心靈投影至沒有盡頭的宇宙最深處。

以下重發最早的 “ 概率權 ” 一文。

一道趣題的 8 個解答

如下，一道 ” 簡單 ” 的選擇題。你按紅色按鈕？還是綠色？

這道題比想像中有趣，我試著回答一下:

根據期望值理論，綠色按鈕價值 5 千萬；
很多人仍然願意選拿到確認的 100 萬，因為他們無法忍受 50% 機率的什麼都拿不到；
換而言之，假如一個人無法承受 “ 什麼都沒有 ” ，那麼右邊的選擇就相當於 “ 你有 50% 機率得到一個億，有 50% 機率死掉 ” 。你當然無法承受死，何況高達 50% 機率；
開放地想，假如你擁有這個選擇的權利，你可將右側價值五千萬的選擇權賣給一個有承受力的人，例如兩千萬（甚至更高）賣給他；
繼續優化上一條，考慮到增加 “ 找到願意購買你該選擇權利的人 ” 的可能性，你可以只用 100 萬（低首付）賣掉這個權利，但要求購買者中得一個億時和你分成；
再進一步，你可以把這個選擇權做成彩票公開發行，將選擇權切碎了零售，兩塊錢一張，印兩億張。頭獎一個億。對比 5 ，風險更低，收益更大；
鑑於 6 的成功商業模式，開始募集下一筆一個億作為頭獎，令其成為一項生意。
按照P／E估值，募集 20 億，公開上市，市值 100 億。

三個風險決策概念

從 100 萬到 100 億，讓我們跳出腦筋急轉彎遊戲，研究一下背後嚴肅的數學原理。經濟學裡有三個風險決策概念：期望值，期望效用，展望理論。

期望值：在機率論和統計學中，一個離散性隨機變量的期望值（或數學期望、或均值，亦簡稱期望，物理學中稱為期待值）是試驗中每次可能結果的機率乘以其結果的總和。換句話說，期望值是隨機試驗在同樣的機會下重複多次的結果計算出的等同 “ 期望 ” 的平均值。（來自維基百科）

例如，擲一枚六面骰子，其點數的期望值是 3.5 ，計算如下：

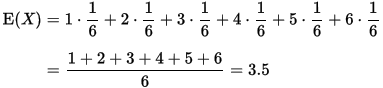
期望效用：在微觀經濟學、博弈論、決策論中，期望效用是一個效用理論，指在風險情況下，個人所作出的選擇是追求某一數量的期望值的最大化。該假說用於解釋賭博和保險中的期望值。（該概念為解決 “ 聖彼得堡悖論 ” 而生）

展望理論： 1970 年代，卡尼曼和特沃斯基系統地研究展望理論。長久以來，主流經濟學都假設每個人作決定時都是 “ 理性 ” 的，然而現實情況並不如此；而展望理論加入了人們對賺蝕、發生機率高低等條件的不對稱心理效用，成功解釋了許多看來不理性的現象。

基於以上理論基礎，我想拋出幾個自覺有趣的結論：

反人性的 “ 每一步都按照整體最優機率做決策 ” ，是傳統意義上成功人士的第一秘密；
窮人將自己的 “ 概率權 ” 廉價賣給了富人，概率權是更隱蔽、更大筆的剩餘價值剝削（並不代表我認同剩餘價值的概念）；
當下熱門的人工智慧，就是依靠每一步都獨立、冷血的計算最優機率，從而戰勝人類。例如 AlphaGo ；
然而，非理性，衝動，有可能成為人類最後的堡壘。（我以後會單獨寫這個）

先過一遍基礎概念。

期望值理論（智者的基本決策工具）

根據期望值理論， 100% 機率得到 5,000 萬，和 50% 機率得到一個億，是一回事情。貝氏定理，是聰明的決策者使用頻率最高的簡單公式之一。

說明： “ 用虧損的機率乘以可能虧損的金額，再用獲利機率乘以可能獲利的金額，最後用後者減去前者。這就是我們一直試圖做的方法。這種算法並不完美，但事情就這麼簡單。 ” （By 巴菲特）

舉例A：（來自高盛前 CEO 魯賓的傳記）
“ 在兩家公司宣布合併後，烏尼維斯的股票交易價為 30.5 美元（合併宣布前為 24.5 美元）。這意味著如果合併事宜談妥的話，來自套利交易的股價上漲可能 3 美元，因為烏尼維斯公司每股股票將會值 33.5 美元（ 0.6075 ×貝迪公司每股股票的價格）。如果合併沒有成功，烏尼維斯公司的股票有可能回落到每股大約 24.5 美元。我們購進的股票有可能下跌 6 美元左右。

我們把合併成功的可能性定為大約 85% ，失敗的可能性為 15% 。在預期價值的基礎上，股價可能上漲的幅度是 3 美元乘以 85% ，而下跌的風險是 6 美元乘以 15% 。
3 美元× 85% =（可能上漲） 2.55 美元
– 6 美元× 15% =（可能下跌）- 0.9 美元
所以，預期價值= 1.65 美元

這 1.65 美元就是我們希望透過把公司 30.50 美元資本擱置三個月所得到的收益。這就算出了可能的報酬率為 5.5% ，或者以年度計算的話為 22% 。比這樣的報酬率再低一些就是我們的底線。我們認為不值得為了低於 20% 的年報酬率而支付我們公司的資本。 “ 魯賓特別解釋道，這就是他每天要做的事情，看起來似乎是賭博，而且的確也經常會輸掉。但他要確保的，是大多數時候賺錢。

舉例B：（來自《黑天鵝》作者）
塔勒佈在投資研討會說： “ 我相信下個星期市場略微上漲的機率很高，上漲機率大概 70% 。 ” 但他卻大量賣空標準普爾 500 指數期貨，賭市場會下跌。他的意見是：市場上漲的可能性比較高（我看好後市），但最好是賣空（我看壞結果），因為萬一市場下跌，它可能跌幅很大。

分析如下：假使下個星期市場有 70% 的機率上漲， 30% 的機率下跌。但是如果上漲只會漲 1% ，下跌則可能跌 10% 。
未來預期結果是： 70% × 1% + 30% ×（- 10% ）=- 2.3% 。
因此應該賭跌，賣空股票獲利的機會更大。如蒙格所言，巴菲特每天做的，都是算這個簡單數學問題。與其說是一種數學能力，不如說是一種思維模式。知道容易，做到極難。

舉例C：
機率有時候顯得 “ 反直覺 ” 。一輛出租車在雨夜肇事，現場有一個目擊證人說，看見該車是藍色。已知：

該目擊證人識別藍色和綠色出租車的準確率是 80% ；
該地的出租車 85% 是綠色的， 15% 是藍色的。

請問：那輛肇事出租車是藍色的機率有多大？
答：該車是綠車但被看成藍車的機率是（ 0.85 × 0.2 ），該車是藍車且被看成藍車的機率是（ 0.15 × 0.8 ），所以該車真的是藍車的機率是（（ 0.15 × 0.8 ）／【（ 0.85 × 0.2 ）+（ 0.15 × 0.8 ）】= 41.38% ）。即，該車更可能是綠色的。

會不會和你的大腦直覺有些差異？我們的大腦做工雖然非常令人驚嘆，但在有些數學直覺方面，顯得非常稚嫩。然而，期望值理論無法回答，為什麼紅色按鈕價值低到 100 萬，仍然有很多人選擇？

期望效用理論（野心或者恐懼）

丹尼爾・伯努利在 1738 年的論文裡，以效用的概念，來挑戰以金額期望值為決策標準，論文主要包括兩條原理：

邊際效用遞減原理：一個人對於財富的佔有多多益善，即效用函數一階導數大於零；隨著財富的增加，滿足程度的增加速度不斷下降，效用函數二階導數小於零。
最大效用原理：在風險和不確定條件下，個人的決策行為準則是為了獲得最大期望效用值而非最大期望金額值。

回到文頭的案例。選擇紅色按鈕，立即變現 100 萬，放棄價值 5,000 萬的選擇權，一方面是因為 “ 滿足於 ” 100 萬，就其財富而言， 100 萬已經帶來數量級的變化，能解決當下最大的難題，足夠心滿意足。而再多一個數量級， 5,000 萬能幹嘛呢？可能也想像不到；另一方面，是想規避綠色按鈕 50% 的歸零風險。對歸零的恐懼感，遠大於多拿到 4,900 萬的期望。確切說，選擇紅色按鈕，交織著 “ 期望效用理論 ” 與 “ 前景理論 ” 的綜合作用。

前景理論

《別做正常的傻瓜》引用因前景理論獲得諾獎的卡尼曼的總結：

在得到的時候，人們都是風險規避的；
在失去的時候，理性者是風險規避的， “ 正常的傻瓜是 ” 是風險偏好的；
理性的決策者對得失的判斷不受參照點的影響，而 “ 正常的傻瓜 ” 對得失的判斷往往根據參照點決定；（例如理性決策者不會非要等到回本才拋掉一支應該拋掉的股票）
正常的傻瓜通常是損失規避的。

如同業為經濟學所研究的，社會、認知與情感的因素，會令人作出不那麼 “ 理性 ” 的選擇。例如，財富的基數，作為參照點，極大程度上決定了人們去按紅色和綠色。

笨人放棄的概率權

笨人不懂得機率的基本常識，不會算期望值（基於三種理論之一）。

誤解 1 ：不懂 “ 大數定律 ”
在數學與統計學中，大數定律又稱大數法則、大數律，是描述相當多次數重複實驗的結果的定律。根據這個定律知道，樣本數量越多，則其平均就越趨近期望值。笨人總想在賭場裡賺錢，而賭場恰恰是大數定律的堅定贏家。

誤解 2 ：賭徒謬誤
特沃斯基和卡尼曼總結：在實際生活中，人們會錯誤地將每次隨機試驗之間獨立的機率建立起聯繫。用擲硬幣的例子來說，我們知道每次拋出得到正反面的機率都是 1 ／ 2 ，但總有人會認為如果連續幾次都得到正面，那麼下次得到反面的機率就會更大。人們常常以為在整體上符合期望的機率分布，在局部上也會符合相同的機率。這種將從大樣本中得到的規律錯誤應用於小樣本中的現象，被稱為 “ 小數定律 ” 。回想 2015 年股災，給股民帶來致命打擊的，是抄底。跌了這麼狠了，總該有次像樣反彈吧。這也算是賭徒謬誤的一種。

誤解 3 ：倖存者偏差
其含義是：根據以事件倖存者為樣本所做出的統計分析是存在偏差的，因為失敗者（或者說是 “ 遇難者 ” ）沒能入選樣本（《黑天鵝》中的沉默證據），所以，以倖存者為樣本所代表的整體是存在偏差（甚至是錯誤）的。

誤解 4 ：鮮活性效應
人們過分看重更鮮活和更容易從記憶中提取出來的證據。誰該向誰道 “ 一路平安 ” ？朋友B開車 20 公里送A去機場，A將從那裡飛往 750 公里以外的某城。離別時，朋友B會對A說： “ 一路平安 ” 。諷刺的是，B回家的 20 公里車程，死於交通事故的機率，比A乘坐航班不幸遇難的機率高出三倍多。然而，受 “ 鮮活性效應 ” 的影響，仍然是B為A祝福。

窮人放棄的概率權

窮人急於變現，無法做到滿足延遲，對效用的期望過低。

哈佛教授塞德希爾在《稀缺》一書中闡述到：我們陷入了稀缺的困境。每個人一旦面臨稀缺狀態，不管是時間還是金錢稀缺，我們都會走入 “ 管窺 ” 狀態，進而引發我們的稀缺心態，稀缺心態容易引發短視和向未來借債。最終我們陷入越來越窮，越來越忙的困境。

曾經和一位老兄聊天，他說，我們最缺的，其實就是有個老爸告訴自己你很牛逼。為何書香門第或者財富世家會出許多偉人，除了基因，資源，可能還有以下原因：

有足夠高的參照點，不會被小利益勾走，更能承受風險（其實是低機率的），從而捕獲高回報；
身邊一群人的示範效應；
被點燃的內心激勵。

他們比窮人更不容易 “ 廉價 ” 甩賣自己的概率權。所以：

貧富差距的關鍵決策點上， “ 窮人 ” 放棄了自己的概率權益；
所謂贏家的秘密就是，堅持按照優勢機率行事，哪怕屢屢受挫也不更改人生下注的原則；
買彩票是最為昂貴的關於機率選擇權的自暴自棄，所以被稱為收智商稅。

錢多的話就價值投資，錢少的話就賭一把。——這可能是投資領域最被廣泛實施的愚蠢。小機率的事情很難實現，看起來反而容易；高機率的事情則顯得路途遙遠，其實到達目的地的可能性要大得多。放棄自己的概率權，選擇舒適的小機率，其實是在用自己本來就微薄的資源，去補貼 “ 成功者 ” 。

聰明人放棄的概率權

換句話說：聰明人為什麼幹蠢事？聰明人既能精確地算出期望值，又野心勃勃，為什麼也會失去自己的概率權，無法在現實世界中過好這一生？

聰明人也無法躲過行為經濟學家嘲諷的那些 “ 愚蠢 ” 行為；
大多數聰明人患有 “ 認知障礙症 ” ，理智上想明白的事情，情感上死活沒法接受；
先入為主，自作聰明；
沒有將正確的思維方式內化為一種行為習慣。

假如人生是一場機率遊戲，假如我們的一連串選擇決策決定了最終結局，那麼，聰明人貌似該有 “ 先天優勢 ” 。而事實並非如此。機率來自賭博。帕斯卡和費馬對賭博奇特結果的興趣，引發他們提出了一些機率論的原理，從而創立了機率論。

以賭場玩家 “ 不輸 ” 機率最高的 21 點為例，賺錢的秘密是：

選一個 “ 友好 ” 的賭場（相當於選對產業）；
對玩兒法基本功滾瓜爛熟；
如電影《決勝 21 點》般數牌；
在優勢機率下，加大下注；
不管結果如何，始終如一地執行以上策略，情緒不波動。

聰明人能夠做好 1-4 。但是對於 “ 反人性 ” 的 5 ，是許多聰明人的弱點。在賭場，你要面對各種干擾，例如：最好的下注時機卻沒有位置，隔壁賭客的抽煙，大胸美女的晃眼，以及擔心害怕。

每個贏家都是一個人肉 AlphaGo

Google 技術團隊與職業棋手，聯合研究了 AlphaGo 對李世乭的棋譜，從中能看到 “ 人工智慧 ” 在進行這項人類最難智力遊戲時，到底是如何思考的。AlphaGo 幾乎會在每一手棋時，都計算自己的贏棋機率。即：對它而言，每一個決策點都是獨立的， AlphaGo 都會冷靜的尋找 “ 當下 ” 的最大獲勝機率。

如本文前面所提及的魯賓、塔勒布、巴菲特，他們差不多都是一個人肉 AlphaGo ，堅持按照機率行事，經常看起來是 “ 反直覺、反人性、反舒適 ” 的。絕大多數聰明人，還沒有這種智慧，以及偉大的行事方式。

被收彩票智商稅的蠢人，和懂得機率但不能堅定實施的聰明人，又都無法逃脫一個陷阱：慾望。在強烈的慾望面前，聰明人認為自己的運氣會提升自己的機率。笨人認為勤能補拙。所謂成功者的確非常勤奮，但此非充分條件。成功者是選擇的結果，其成功秘密都是事後歸因。所以，有另外一種比智商稅更隱蔽的稅：發財夢稅。這能解釋兩個常見 “ 經濟現象 ” ：

為什麼中國的商業街總在裝修、換商家？（對比而言，國外的商家很少變遷）
為什麼大量淘寶店主們願意為一份低於薪資的收入， 24 小時勤奮工作著？

街頭頻換換手之商舖的過高租金，網路上創業者不計回報的拼搏，正是在為發財夢付出溢價。

你如何定義自己的 “ 賭場 ”

祖克柏不過是中產家庭出身。他仍能在公司成立兩年的困難階段，拒絕了雅虎（母公司 Verizon,VZ-US）的 10 億美元收購。這是一個艱難的決定。幾年以後，祖克柏對記者說，拒絕收購的一年內，幾乎所有的高層全部走光了。

你是馬上就拿到 10 個億，還是以百分之幾的可能性在數年之後拿到 1,000 個億？——這個擺在祖克柏面前的選擇，多麼像本文開篇那個按鈕選擇。比較而言，祖克柏的綠色按鈕（失去懲罰）要殘忍得多。秘密在於，擺在祖克柏面前的，並非 10 億和 1,000 億的選擇，而是堅持或放棄夢想的選擇。數年後，snapchat 以類似的方式拒絕了祖克柏的 30 億美元收購要約。

無論結局如何，這便是矽谷的精神之一。僅靠發財夢，很難驅動太大的事業。財富觀、雄心壯志、年輕氣盛，超越經濟動物的貪婪，讓他們按下了成功機率遠低於 50% 的綠色按鈕。

如何不賤賣選擇權？

許多人生選擇題，除了abcd，還可能有一個 “ 其它 ” 選項。對了對付德國人的密碼機，圖靈決定 “ 以機攻機 ” ，然而領導不批預算，並喝令他服從上級命令。圖靈同學靈機一動問：你的上級是誰？隨後給丘吉爾寫了封信搞掂十萬英鎊。我可以按紅色，也可以按綠色，意味著我擁有選擇權。我可否有另外的變現渠道呢？第三條路，出賣選擇權，將其賣給 VC 和 PE，是利用資本的風險喜好與承受力，分享了 100 萬與 5,000 萬之間的價值地帶。

有趣的是，財富世界為一窮二白的年輕人留下了一個暗門。他們並不因自己渴望 100 萬而非得錯失 5,000 萬。他們只需要更廣闊的視野。這是當下社會財富的創造與分配核心驅動力之一。亦為資本的美妙之處。對於 “ 選擇權 ” 的決策思想與行動模式，決定了最終的財富食物鏈。

成功學的機率常識

假如你在一個正確的區域，下面一定有金礦（這也是個偽命題，地球下面是有金礦，界定的精確性呢？）然後你重複試錯，聰明地試錯，這些試錯可以積澱和滾雪球般，不斷提升你的成功機率。

引用一個雞湯段子：如果一件事的成功率是 1% ，反覆嘗試 100 次，至少成功 1 次的機率是多少？答案：如果成功率是 1% ，意味著失敗率是 99% 。按照反覆嘗試 100 次來計算，那失敗率就是 99% 的 100 次方，約等於 37% ，最後我們的成功率應該是 100% 減去 37% ，即 63% 。一件事倘若反覆嘗試，它的成功率竟然由 1% 奇蹟般地上升到不可思議的 63% 。

前面說過了，勝率不佔優時，不要反覆押注。如果這麼做，根據大數定律，會輸得精光。但為什麼上面的成功學公式卻可以實現反轉呢？原因在於，你在賭場輸的是錢。而在成功學的反轉公式裡，是假設你的時間成本、精力成本、機會成本、金錢成本都忽略了。你需要不服輸，你的體力好很重要，你還願意投入時間，這些都是你的成本。有些人不會因為反覆挫敗而喪失精力。每次重新開始的時候，他都如第一次般充滿激情。每一次他都準備好了。由上，人生的錯誤不是算錯了數學機率，不然就是反覆的次數不夠多，或是經不起折騰。所以，吃苦，可能是最核算的、可以反覆押上的籌碼，尤其適合年輕的人生賭徒們。

美國史丹佛大學工程教授羅伯特・桑頓說：在創造過程中，天縱其才未必比生產能力重要。發現一個有用的好想法，你先要去嘗試許多沒用的。這是個純粹的數字遊戲。

有本書專門探討過該問題：如果創新者本人對他們自身想法做出的評判並不可靠，他們怎樣才能提高創作出傑作的機率呢？答案是：他們想出大量的創意。西蒙頓發現，平均而言，創意天才在他們所在領域的作品並不比同業的作品質量更好，他們只是有大量的想法罷了。這給他們更多的變化，更高的獲得獨創性的機會。

“ 一個人能想出有影響力的成功創意的機率， ” 西蒙頓指出， “ 同他想出的創意總數成正比。 ”

例如莎士比亞：我們對他的一小部分經典作品耳熟能詳，但卻忘記了在 20 年中，他創作了 37 部戲劇和 154 首十四行詩。

如何當一個成功的 CEO ？在這裡，作者霍洛維茨分享了一條重要的經驗：創業公司的 CEO 不應該計算成功的機率。創建公司時，你必須堅信，任何問題都有一個解決辦法。而你的任務就是找出解決辦法，無論這一機率是十分之九，還是千分之一，你的任務始終不變。他還認為：當一名成功的 CEO 根本沒有秘訣。如果說存在這樣一種技巧，那就是看其專心致志的能力和在無路可走時選擇最佳路線的能力。與普通人相比，那些令你最想躲藏起來或者乾脆撕掉的時刻，就是你作為一名 CEO 所要經歷的不同於常人的東西。

“ 只要肯幹，你一定可以出人頭地。要敢於 All in。 ” 這些都是當下流行的人生觀。結合上面的成功機率計算，我們要奮不顧身地為未來下注嗎？仍然是要看你手中的籌碼。在我們的一生中，面對不確定性，我們大多時候扔骰子的次數都是有限的，並且是消耗資源的。永不放棄，指的是你的鬥志，而非押完你錢包裡的最後一塊錢。

錢少就該去賭一把嗎？

由此可以探討兩個經常被誤讀的話題：

錢少的投資者就該買高風險的股票嗎？
當你的籌碼是 “ 有限的 ” 錢時，錢少的人和錢多的人，只是數字上的區別，下注應該以比例、而非金額來區隔。有些人覺得自己錢少，慢慢搞來不及，所以要冒險。這和想去賭場提款一樣愚蠢（除非你是數學博士）。難道錢少就可以不遵循機率的法則？難道錢少就要去賭場，活生生把自己推入大數定律的絞肉機？這就是為什麼 “ 窮人 ” 常自暴自棄，快速地賭掉了最後的籌碼。

創業者是在賣 “ 命 ” 。
接著上個話題， “ 我手上就兩千塊，即使按照巴菲特的報酬率，我這輩子也買不起房啊？ ” 回答：

假如你用錢做籌碼，你就要遵循錢的機率原則；
你還可以有另外的籌碼，以另外的下注方式，賣命。

也就是：賣掉你的命運，以及動腦、吃苦、拼命。創業仍然是小機率事件。即使你的智慧、精力、時間是零成本，即使你不斷試錯、不斷探索，讓你的成功率越來越高，最後跑出來的也不多。大公司的創新，很多時候不比創業者成功率更高。所以他們買入那些跑贏了的創業公司。某種意義上，他們就是買創業者 “ 小荷才露尖尖角的好命 ” ，避免自己付出大公司極高的試錯成本。

人生選擇有限

人生有很多個選擇時刻，不能總是被 “ 機率 ” 和 “ 最優 ” 驅使。就像《怒海爭鋒》裡，傑克船長暫時放棄追殺敵船，選擇停靠小島，滿足船醫夢寐以求的達爾文式科學考察。想起一個朋友，夫妻選擇將創業和置業延後，將時間留給成長中的孩子。許多美好事物和美好時刻，都是因為一些 “ 不計算 ” 的選擇。

安德烈・高茲說： “ 我開始思考，什麼是應該放棄的次要的東西，放棄了它我才能集中精力追求最重要的。而追根究柢，只有一件事對我來說是最主要的：那就是和你在一起。 ” 當然，最好我們手上有足夠的、靠 AlphaGo 機率計算法贏得的籌碼，供自己去揮霍，或是幫助那些沒有人生賭場權的人。例如蓋茲的慈善基金。

也許選擇本身比財富更重要。如果說時光是最寶貴的財富，比時光還有限的人生選擇呢？我想起 1995 年畢業後獨自去廣州，遇到一位師長，他見我有些無師自通的靈性，不吝在旁人面前贊 “ 這是天才少年 ” 。（時光總是嫌老愛幼，迄今為止尚未有人稱我是天才中年。）他註冊自己公司的時候，頭疼選名，於是說：不如就叫 “ 選擇 ” 。於是這公司成為我加入的第一間公司，其名字蘊含著廣泛的人生隱喻：

“ 選擇有限 ” 公司。

https://www.stockfeel.com.tw/概率權-機率-有錢人/